Note
This tutorial was generated from an IPython notebook that can be downloaded here.
Implementing new kernels#
This notebook was made with the following version of george:
import george
george.__version__
'0.3.1'
All the kernels used by george must be implemented in C++ with Python bindings. This means that you need to recompile the code anytime you want to add a new kernel. This is an unavoidable PITA but—as of version 1.0—george comes with a kernel specification language that is designed to make this process as painless as possible.
To follow this tutorial, you’ll need the development version of george. You should follow the instructions here to get that set up and once you can build the code, let’s start implementing a new kernel.
The kernel function#
In this tutorial, we will work through the implementation of a kernel
that wasn’t available in early versions of the code: the
LocalGaussianKernel. This kernel has been used by Ian
Czekala in his stellar spectrum fitting
algorithm Starfish.
This kernel is not stationary and its value is given by the following equation:
where the parameters \(x_0\) and \(w\) are the location and width of the Gaussian respectively. We’re actually going to parameterize this kernel using \(\ln w\) instead of \(w\) because it must be strictly positive.
In our implementation, we’ll also need the derivatives of this function with respect to the hyperparameters so let’s list those now:
and
Kernel specification#
In the root directory of your development version of george, there
should be a directory called kernels. In this directory, create a
new file called MyLocalGaussian.yml and edit it to have the
following contents:
name: MyLocalGaussianKernel
doc: You should always document your code.
stationary: false
params: [x0, log_w]
reparams:
inv_2w: return 0.5 * exp(-log_w);
value: |
double d1 = x1 - x0, d2 = x2 - x0;
return exp(-(d1*d1 + d2*d2) * inv_2w);
grad:
x0: |
double d1 = x1 - x0, d2 = x2 - x0;
return 2 * exp(-(d1*d1 + d2*d2) * inv_2w) * inv_2w * (d1 + d2);
log_w: |
double d1 = x1 - x0, d2 = x2 - x0,
arg = (d1*d1 + d2*d2) * inv_2w;
return exp(-arg) * arg;
x1: |
double d1 = x1 - x0, d2 = x2 - x0;
return -2.0 * exp(-(d1*d1 + d2*d2) * inv_2w) * d1 * inv_2w;
x2: |
double d1 = x1 - x0, d2 = x2 - x0;
return -2.0 * exp(-(d1*d1 + d2*d2) * inv_2w) * d2 * inv_2w;
This file is written in a markup language called YAML and there are a lot of online resources for the details of the syntax but let’s go through it line-by-line now to explain what’s going on.
The
namefield is the name that you want the Python class to have. The convention is to have it end inKernelbut I guess you can call it more-or-less anything.The
docfield let’s you write a docstring for the class. This is always a good idea and you can look at the existing kernels for inspiration.This kernel is not stationary and you specify that using the
stationaryfield.paramslists the “natural” parameters of the kernel. The derivatives should be computed with respect to these parameters.It is often useful (for speed) to pre-compute a reparameterized form of the parameters. In this case, we don’t want to make too many calls to the
expfunction so we’ll pre-compute \((2\,w)^{-1}\). To do this, we add an entry to thereparamsdictionary with raw C++ code for a function that returns the reparameterization. This function will take the natural parameters as input so you can use them directly by name.The
valueentry gives the raw C++ code for evaluating the kernel function at inputdoublesx1andx2. This function will take the parameters and the reparameterizations as inputs so you can use them by name.Finally, the
graddictionary gives the raw C++ code for computing the gradient as a function of each parameter.
After you save this file and recompile george, you should now have access to this kernel as follows:
import numpy as np
from george import kernels
kernel = 5 * kernels.MyLocalGaussianKernel(x0=0.0, log_w=np.log(0.2))
kernel += 5 * kernels.Matern32Kernel(100.0)
Whenever you implement a new kernel, you should numerically test that
you’ve implemented the gradients correctly. The Kernel
implementation includes a function for doing exactly that and here’s how
you would call it:
x = np.linspace(-10, 10, 500)
kernel.test_gradient(np.atleast_2d(x).T)
If our implementation was wrong, this would have raised an exception so this looks pretty promising!
Now, we can plot the covariance matrix given by this kernel as follows:
import matplotlib.pyplot as pl
k = kernel.get_value(np.atleast_2d(x).T)
pl.figure(figsize=(6, 6))
pl.imshow(k, cmap="gray", interpolation="nearest")
pl.gca().set_xticklabels([])
pl.gca().set_yticklabels([]);

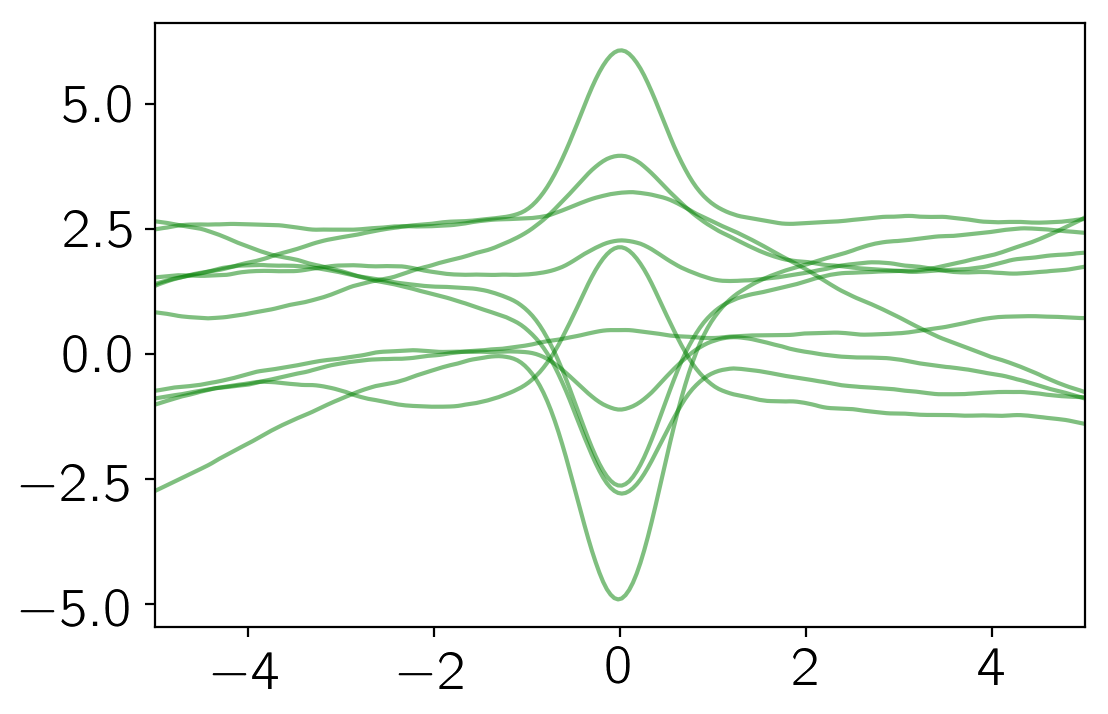
From this covariance function, we can sample some representative functions:
np.random.seed(123)
gp = george.GP(kernel)
gp.compute(x)
y = gp.sample(size=10)
pl.plot(x, y.T, "g", lw=1.5, alpha=0.5)
pl.xlim(-5, 5);
George already includes an implementation of this kernel (called the
LocalGaussianKernel) so we’ll finish here but when you implement
your own favorite kernel, you should now open a pull request to include
the kernel in the released version of george.