Note
This tutorial was generated from an IPython notebook that can be downloaded here.
Mixtures of GPs#
This notebook was made with the following version of george:
import george
george.__version__
'0.3.1'
It can be useful to model a dataset using a mixture of GPs. For example, the data might have both systematic effects and a physical signal that can be modeled using a GP. I konw of a few examples where this method has been used in the context of time series analysis for the discovery of transiting exoplanets (for example, Aigrain et al. 2016 and Luger et al. 2016), but I’m sure that these aren’t the earliest references. The idea is pretty simple: if your model is a mixture of two GPs (with covariance matrices \(K_1\) and \(K_2\) respectively), this is equivalent to a single GP where the kernel is the sum of two kernels, one for each component (\(K = K_1 + K_2\)). In this case, the equation for the predictive mean conditioned on a dataset \(\boldsymbol{y}\) is
where \(N\) is the (possibly diagonal) matrix describing the measurement uncertainties. It turns out that the equation for computing the predictive mean for component 1 is simply
and the equivalent expression can be written for component 2.
This can be implemented in george using the new kernel keyword
argument in the predict method. To demonstrate this, let’s start by
generating a synthetic dataset. Component 1 is a systematic signal that
depends on two input parameters (\(t\) and \(\theta\) following
Aigrain) and component 2 is a quasiperiodic oscillation that is the
target of our analysis.
import numpy as np
import matplotlib.pyplot as plt
from george import kernels
np.random.seed(42)
N = 256
t = np.sort(np.random.uniform(0, 10, N))
theta = np.random.uniform(-np.pi, np.pi, N)
X = np.vstack((t, theta)).T
yerr = np.random.uniform(0.05, 0.25, N)
kernel1 = 2.0 * kernels.Matern32Kernel([5.0, 0.5], ndim=2)
kernel2 = 2.0 * kernels.ExpSine2Kernel(gamma=10.0, log_period=np.log(5.), ndim=2, axes=0)
kernel2 *= kernels.ExpSquaredKernel([15.0], ndim=2, axes=0)
kernel = kernel1 + kernel2
gp = george.GP(kernel)
y = gp.sample(X)
y += yerr * np.random.randn(N)
gp.compute(X, yerr)
plt.errorbar(t, y, yerr=yerr, fmt=".k", capsize=0)
plt.ylim(-6.5, 6.5)
plt.xlim(0, 10)
plt.xlabel("t")
plt.ylabel("y");

The physical (oscillatory) component is not obvious in this dataset because it is swamped by the systematics. Now, we’ll find the maximum likelihood hyperparameters by numerically minimizing the negative log-likelihood function.
from scipy.optimize import minimize
def nll(params):
gp.set_parameter_vector(params)
l = gp.log_likelihood(y, quiet=True)
g = gp.grad_log_likelihood(y, quiet=True)
return -l, -g
params = gp.get_parameter_vector()
params += 0.05*np.random.randn(len(params))
soln = minimize(nll, params, jac=True)
gp.set_parameter_vector(soln.x)
print(soln.success, soln.x)
True [ 0.38315985 1.88867446 -0.35673864 -0.33250025 11.98452994
1.59429178 2.11371316]
Now let’s use the trick from above to compute the prediction of component 1 and remove it to see the periodic signal.
# Compute the predictive means - note the "kernel" argument
mu1 = gp.predict(y, X, return_cov=False, kernel=kernel1)
mu2 = gp.predict(y, X, return_cov=False, kernel=kernel2)
plt.plot(t, y, ".k", mec="none", alpha=0.3)
plt.plot(t, y - mu1, ".k")
plt.plot(t, mu2)
plt.ylim(-6.5, 6.5)
plt.xlim(0, 10)
plt.xlabel("t")
plt.ylabel("y");
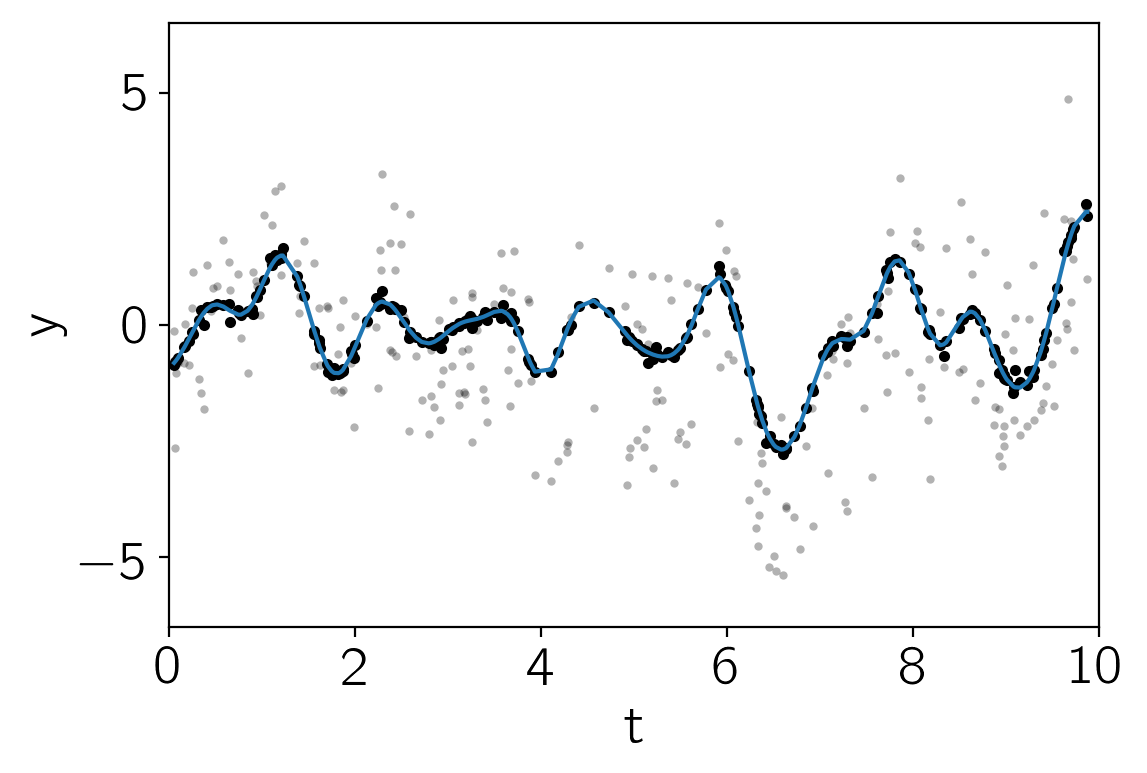
In this plot, the original dataset is plotted in light gray points and the “de-trended” data with component 1 removed is plotted as black points. The prediction of the GP model for component 2 is shown as a blue line.